- Урок 19. Электрическое сопротивление материалов
- Урок 20. Закон Ома для участка цепи
- Урок 21. Расчет сопротивления проводника. Удельное сопротивление
- Урок 22. Реостаты
- Урок 23. Последовательное соединение проводников
- Урок 24. Параллельное соединение проводников
- Урок 25. Работа электрического тока
- Урок 26. Мощность электрического тока
- Урок 27. Единицы работы электрического тока, применяемые на практике
Урок 19. Электрическое сопротивление материалов
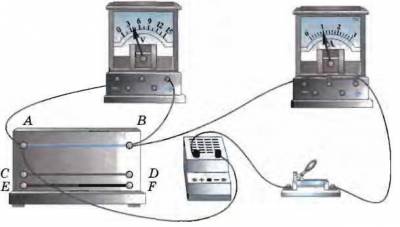
Включая в электрическую цепь какого-нибудь источника тока различные проводники и амперметр, можно заметить, что при разных проводниках показания амперметра различны, т. е. сила тока в данной цепи различна. Так, например, если вместо железной проволоки АВ включить в цепь такой же длины и сечения никелиновую проволоку С£>, то сила тока в цепи уменьшится, а если включить медную ЕР, то сила тока значительно увеличится.
Вольтметр, поочередно подключаемый к концам этих проводников, показывает одинаковое напряжение. Значит, сила тока в цепи зависит не только от напряжения, но и от свойств проводников, включенных в цепь. Зависимость силы тока от свойств проводника объясняется тем, что разные проводники обладают различным электрическим сопротивлением.
Электрическое сопротивление — физическая величина. Обозначается оно буквой R.
За единицу сопротивления принимают 1 ом — сопротивление такого проводника, в котором при напряжении на концах 1 вольт сила тока равна 1 амперу. Кратко это записывают так:
1Om=1V/1A
Применяют и другие единицы сопротивления: миллиом (мОм), килоом (кОм), мегаом (МОм).
1 мОм = 0,001 Ом;
1 кОм = 1000 Ом;
1 МОм = 1 000 000 Ом.
В чем причина сопротивления? Если бы электроны в проводнике не испытывали никаких помех в своем движении, то они, будучи приведены в упорядоченное движение, двигались бы по инерции неограниченно долго. В действительности электроны взаимодействуют с ионами кристаллической решетки металла. При этом замедляется упорядоченное движение электронов и сквозь поперечное сечение проводника проходит за 1 с меньшее их число. Соответственно уменьшается и переносимый электронами за 1 с заряд, т. е. уменьшается сила тока. Таким образом, каждый проводник как бы противодействует электрическому току, оказывает ему сопротивление.
Причиной сопротивления является взаимодействие движущихся электронов с ионами кристаллической решетки.
Разные проводники обладают различным сопротивлением из-за различия в строении их кристаллической решетки, из-за разной длины и площади поперечного сечения.
Урок 20. Закон Ома для участка цепи
В предыдущих параграфах были рассмотрены три величины, с которыми мы имеем дело в любой электрической цепи, — это сила тока, напряжение и сопротивление. Эти величины связаны между собой. Зависимость силы тока от напряжения мы уже установили. Мы уже знаем, что сила тока в проводнике прямо пропорциональна напряжению на концах проводника. Обратите внимание, что при проведении опыта сопротивление проводника не менялось.
При проведении физических опытов, в которых определяют зависимость одной величины от другой, все остальные величины должны быть постоянными. Если они будут изменяться, то установить зависимость будет сложнее. Поэтому, определяя зависимость силы тока от сопротивления, напряжение на концах проводника надо поддерживать постоянным.
Чтобы ответить на вопрос, как зависит сила тока в цепи от сопротивления, обратимся к опыту.
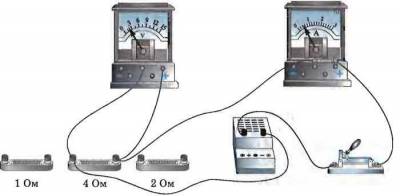
На рисунке изображена электрическая цепь, источником тока в которой является аккумулятор. В эту цепь по очереди включают проводники, обладающие различными сопротивлениями. Напряжение на концах проводника во время опыта поддерживается постоянным. За этим следят по показаниям вольтметра. Силу тока в цепи измеряют амперметром.
Ниже приведены результаты опытов с тремя различными проводниками.
| № опыта | Напряжение на концах проводника, В | Сопротивление проводника, Ом | Сила тока в цепи, А |
| 1 | 2 | 1 | 2 |
| 2 | 2 | 2 | 1 |
| 3 | 2 | 4 | 0,5 |
Обобщая результаты опытов, приходим к выводу, что сила тока в проводнике обратно пропорциональна сопротивлению проводника.
Зависимость силы тока от напряжения на концах участка цепи и сопротивления этого участка называется законом Ома по имени немецкого ученого Георга Ома, открывшего этот закон в 1827 г.
Закон Ома читается так: сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
здесь I — сила тока в участке цепи, U — напряжение на этом участке, R — сопротивление участка.
Закон Ома — один из основных физических законов.

На рисунке зависимость силы тока от сопротивления проводника при одном и том же напряжении на его концах показана графически. На этом графике по горизонтальной оси в условно выбранном масштабе отложены сопротивления проводников в омах, по вертикальной — сила тока в амперах.
Следовательно, зная силу тока и сопротивление, можно по закону Ома вычислить напряжение на участке цепи, а зная напряжение и силу тока — сопротивление участка.
Сопротивление проводника можно определить по формуле
R = U / I ,
однако надо понимать, что R — величина постоянная для данного проводника и не зависит ни от напряжения, ни от силы тока. Если напряжение на данном проводнике увеличится, например, в три раза, то во столько же раз увеличится и сила тока в нем, а отношение напряжения к силе тока не изменится.
Урок 21. Расчет сопротивления проводника. Удельное сопротивление
Мы знаем, что причиной электрического сопротивления проводника является взаимодействие электронов с ионами кристаллической решетки металла. Поэтому можно предположить, что сопротивление проводника зависит от его длины и площади поперечного сечения, а также от вещества, из которого он изготовлен.
На рисунке изображена установка для проведения такого опыта. В цепь источника тока по очереди включают различные проводники, например:
1) никелиновые проволоки одинаковой толщины, но разной длины,
2) никелиновые проволоки одинаковой длины, но разной толщины (разной площади поперечного сечения);
3) никелиновую и нихромовую проволоки одинаковой длины и толщины.
Силу тока в цепи измеряют амперметром, напряжение — вольтметром.
Как учесть зависимость сопротивления от вещества, из которого изготовляют проводник? Для этого вычисляют так называемое удельное сопротивление вещества.
Удельное сопротивление — это физическая величина, которая определяет сопротивление проводника из данного вещества длиной 1 м, площадью поперечного сечения 1 м2.
В таблице приведены значения удельных сопротивлений некоторых веществ при 20 °С. Удельное сопротивление с изменением температуры меняется. Опытным путем было установлено, что у металлов, например, удельное сопротивление с повышением температуры увеличивается.| Серебро | 0,016 |
| Медь | 0,017 |
| Золото | 0,024 |
| Алюминий | 0,028 |
| Вольфрам | 0,055 |
| Железо | 0.1 |
| Свинец | 0,21 |
При проводке электрических цепей используют алюминиевые, медные и железные провода.
Во многих случаях бывают нужны приборы, имеющие большое сопротивление. Их изготавливают из специально созданных сплавов — веществ с большим удельным сопротивлением. Например, как видно из таблицы, сплав нихром имеет удельное сопротивление почти в 40 раз большее, чем алюминий.
Фарфор и эбонит имеют такое большое удельное сопротивление, что почти совсем не проводят электрический ток, их используют в качестве изоляторов.
Урок 22. Реостаты
На практике часто приходится менять силу тока в цепи, делая ее то больше, то меньше. Так, изменяя силу тока в динамике радиоприемника, мы регулируем громкость звука. Изменением силы тока в электродвигателе швейной машины можно регулировать скорость его вращения.
Во многих случаях для регулирования силы тока в цепи применяют специальные приборы — реостаты.
Простейшим реостатом может служить проволока из материала с большим удельным сопротивлением, например никелиновая или нихромовая. Включив такую проволоку в цепь источника электрического тока через контакты А и С последовательно с амперметром и передвигая подвижный контакт С, можно уменьшать или увеличивать длину включенного в цепь участка АС. При этом будет меняться сопротивление цепи, а следовательно, и сила тока в ней.
Перемещая ползунок по стержню, можно увеличивать или уменьшать сопротивление реостата, включенного в цепь.
Каждый реостат рассчитан на определенное сопротивление и на наибольшую допустимую силу тока, превышать которую не следует, так как обмотка реостата накаляется и может перегореть. Сопротивление реостата и наибольшее допустимое значение силы тока указаны на реостате.
Урок 23. Последовательное соединение проводников
Электрические цепи, с которыми приходится иметь дело на практике, обычно состоят не из одного приемника электрического тока, а из нескольких различных, которые могут быть соединены между собой по-разному. Зная сопротивление каждого и способ их соединения, можно рассчитать общее сопротивление цепи.
На рисунке изображена цепь последовательного соединения двух электрических ламп и схема такого соединения. Если выключать одну лампу, то цепь разомкнется, и другая лампа погаснет.
Последовательно соединены, например, аккумулятор, лампа, два амперметра и ключ в цепи, изображенной на рисунке.
Мы уже знаем, что при последовательном соединении сила тока в любых частях цепи одна и та же, т. е.
I = I1 = I2
А чему равно сопротивление последовательно соединенных проводников?
Соединяя проводники последовательно, мы как бы увеличиваем длину проводника. Поэтому сопротивление цепи становится больше сопротивления одного проводника.
Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников (или отдельных участков цепи):
R=R1+R2
Напряжение на концах отдельных участков цепи рассчитывается на основе закона Ома:
U1=I*R1
U2=I*R2
Из приведенных равенств видно, что напряжение будет большим на проводнике с наибольшим сопротивлением, так как сила тока везде одинакова.
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
U = U1 + U2.
Это равенство вытекает из закона сохранения энергии. Ведь электрическое напряжение на участке цепи измеряется работой электрического тока, совершающейся при прохождении по этому участку цепи электрического заряда в 1 Кл. Эта работа совершается за счет энергии электрического поля, и энергия, израсходованная на всем участке цепи, равна сумме энергий, которые расходуются на отдельных проводниках, составляющих участок этой цепи.
Все приведенные закономерности справедливы для любого числа последовательно соединенных проводников.
Пример 1. Два проводника сопротивлением R1 = 2 Ом, R2 = 3 Ом соединены последовательно. Сила тока в цепи I = 1 А. Определить со-противление цепи, напряжение на каждом проводнике и полное напряжение всего участка цепи.
Запишем условие задачи и решим ее.
Урок 24. Параллельное соединение проводников
Другой способ соединения проводников, применяемый в практике, называется параллельным соединением. На рисунке изображено параллельное соединение двух электрических ламп. Обратите внимание на важные особенности такого соединения.

При параллельном соединении все входящие в него проводники одним своим концом присоединяются к одной точке цепи А, а вторым концом к другой точке В. Поэтому напряжение на участке цепи АВ и на концах всех параллельно соединенных проводников одно и то же:
U = U1 = U2
Очень удобно поэтому применять параллельное соединение потребителей в быту и в технике, так как все потребители в этом случае изготавливаются в расчете на одинаковое напряжение. Кроме того, при выключении одного потребителя другие продолжают действовать, ток в них не прерывается, так как цепь остается замкнутой.
При параллельном соединении ток в точке В разветвляется на два тока I1 и I2, сходящиеся вновь в точке А, подобно тому как поток воды в реке распределяется по двум каналам, сходящимся затем вновь.
Поэтому сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединенных проводниках.
I = I1 + I2.
При параллельном соединении как бы увеличивается площадь поперечного сечения проводника. Поэтому общее сопротивление цепи уменьшается и становится меньше сопротивления каждого из проводников, входящих в цепь. Так, например, сопротивление цепи R, состоящей из двух одинаковых ламп, сопротивлением R1 каждая, в два раза меньше сопротивления одной лампы: R = R1 / 2 . Общее сопротивление цепи при параллельном соединении проводников определяется по формуле
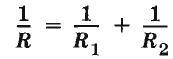
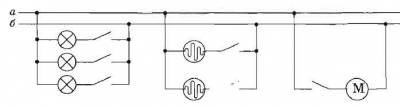
В одну и ту же электрическую цепь параллельно могут быть включены самые различные потребители электрической энергии. На рисунке показано параллельное включение электрических ламп, нагревательных приборов и электродвигателя.
Такая схема соединения потребителей тока используется, например, в жилых помещениях; в точках а и б провода осветительной сети вводятся в квартиру.
Потребители, параллельно включаемые в данную сеть, должны быть рассчитаны на одно и то же напряжение, равное напряжению в сети. Напряжение в сети, используемое у нас для освещения и в бытовых приборах 220 В. Поэтому электрические лампы и различные бытовые электроприборы изготовляют на 220 В.
В практике часто применяется смешанное (последовательное и параллельное) соединение проводников. Зная сопротивления проводников, соединенных параллельно, и напряжение на этом участке цепи, можно определить многие другие электрические величины этой цепи. Для этого нужно использовать формулы: U=U1=U2, I=I1+I2, а также закон Ома для участка цепи.
Пример. В осветительную сеть комнаты включены две электрические лампы, сопротивления которых 200 и 300 Ом. Напряжение в сети 120 В. Определить силу тока в каждой лампе, силу тока в подводящих проводах (т. е. силу тока до разветвления), общее сопротивление участка, состоящего из двух ламп.
Сила тока в подводящих проводах равна сумме сил тока в лампах: I = I1 + I2 = 0,6 А + 0,4 А = 1 А.
Общее сопротивление участка цепи, состоящего из двух параллельно соединенных ламп, находим по закону Ома:
R=U/I
R = 120 V / 1 A=120 Om
7’К = 120 Ом. I -I А Ответ: I1 = 0,6 А, I2 = 0,4 А, I = 1 А, R = 120 Ом.
Решив задачу, мы убедились, что общее сопротивление участка цепи R = 120 Ом, состоящего из двух параллельно соединенных проводников сопротивлением R1 = 200 Ом и R2 = 300 Ом, меньше сопротивления каждого проводника.
Урок 25. Работа электрического тока
Как вычислить работу электрического тока? Мы уже знаем, что напряжение на концах участка цепи численно равно работе, которая совершается при прохождении по этому участку электрического заряда в 1 Кл. При прохождении по этому же участку электрического заряда, равного не 1 Кл, а, например, 5 Кл, совершенная работа будет в 5 раз больше. Таким образом, чтобы определить работу электрического тока на каком-либо участке цепи, надо напряжение на концах этого участка цепи умножить на электрический заряд (количество электричества), прошедший по нему:
А = Uq,
где А — работа, U — напряжение, q — электрический заряд. Электрический заряд, прошедший по участку цепи, можно определить, измерив силу тока и время его прохождения:
q = It.
Используя это соотношение, получим формулу работы электрического тока, которой удобно пользоваться при расчетах:
А = Ult.
Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.
Работу измеряют в джоулях, напряжение — в вольтах, силу тока — в амперах и время — в секундах, поэтому можно написать:
1 джоуль = 1 вольт х 1 ампер х 1 секунду, или 1 Дж = 1 В • А • с.
Выходит, что для измерения работы электрического тока нужны три прибора: вольтметр, амперметр и часы. На практике работу электрического тока измеряют специальными приборами — счетчиками. В устройстве счетчика как бы сочетаются три названных выше прибора. Счетчики электроэнергии сейчас можно видеть почти в каждой квартире.
Пример. Какую работу совершает электродвигатель за 1 ч, если сила тока в цепи электродвигателя 5 А, напряжение на его клеммах 220 В? КПД двигателя 80% .
А1 = 4 ООО ООО Дж * 80% : 100% = 3 200 000 Дж = 3,2 • 106 Дж = = 3,2 • 103 кДж.
Ответ: Ах = 3,2 • 103 кДж.
Урок 26. Мощность электрического тока
Мы знаем, что мощность численно равна работе, совершенной в единицу времени. Следовательно, чтобы найти среднюю мощность электрического тока, надо его работу разделить на время:
где Р — мощность тока.
Работа электрического тока равна произведению напряжения на силу тока и на время: А = UIt.
Таким образом, мощность электрического тока равна произведению напряжения на силу тока, или
Из этой формулы можно определить, что U=P/I, I=P/U.
За единицу мощности, как известно, принят 1 Вт, равный 1Дж/с
Из формулы Р = U*I следует, что
1 ватт = 1 вольт • 1 ампер, или 1 Вт = 1 В • А.
Используют также единицы мощности, кратные ватту: гектоватт (гВт), киловатт (кВт), мегаватт (МВт).
1 гВт = 100 Вт, 1 кВт = 1000 Вт, 1 МВт = 1 000 000 Вт. Измерить мощность электрического тока можно с помощью вольтметра и амперметра. Чтобы вычислить искомую мощность, необходимо напряжение умножить на силу тока. Значение силы тока и напряжение определяют по показаниям приборов.
Существуют специальные приборы — ваттметры, которые непосредственно измеряют мощность электрического тока в цепи. В таблице приведены мощности некоторых источников и потребителей электрического тока.
| Лампа карманного фонаря | = 0,001 |
| Холодильник домашний | 0,110—0,16 |
| Лампы осветительные (бытовые) | 0,015—0,2 |
| Электрический утюг | 0,3—1 |
| Стиральная машина | 0,35—0,6 |
| Электрическая плитка | 0,6; 0,8; 1; 1,25 |
| Электропылесос | до 0,6 |
| Лампы в звездах башен Кремля | 5 |
| Двигатель электровоза ВЛ10 | 650 |
| Электровоз ВЛ10 | 5200 |
| Электродвигатель прокатного стана | 6000—9000 |
| Гидрогенератор Братской ГЭС | 250 000 |
| Турбогенератор | 50 000—1 200 000 |
Урок 27. Единицы работы электрического тока, применяемые на практике
В паспортах приемников тока — лампах, плитках, электродвигателях — обычно указывают мощность тока в них. По мощности легко определить работу тока за заданный промежуток времени, пользуясь формулой А = Р*t.
Выражая мощность в ваттах, а время в секундах, получим работу в джоулях:
1 Вт = 1Дж/с, откуда 1 Дж = 1 Вт • с.
Однако эту единицу работы неудобно использовать на практике, так как в потребителях электроэнергии ток производит работу в течение длительного времени, например в бытовых приборах — в течение нескольких часов, в электропоездах — по нескольку часов и даже суток, а расчет израсходованной энергии по электросчетчику производится чаще всего за месяц. Поэтому при вычислении работы тока или затрачиваемой и вырабатываемой электрической энергии во всех этих случаях приходится переводить эти отрезки времени в секунды, что усложняет расчеты.
Поэтому на практике, вычисляя работу тока, гораздо удобнее время выражать в часах, а работу тока не в джоулях, а в других единицах:
ватт-час (Вт * ч), гектоватт-час (гВт * ч), киловатт-час (кВт * ч).
1 Вт • ч = 3600 Дж;
1 гВт • ч = 100 Вт • ч = 360 000 Дж;
1 кВт • ч = 1000 Вт • ч = 3 600 000 Дж.
Пример. Имеется электрическая лампа, рассчитанная на ток мощностью 100 Вт. Ежедневно лампа горит в течение 6 ч. Найти работу тока за один месяц (30 дней) и стоимость израсходованной энергии при тарифе 30 к. за 1 кВт • ч.
Запишем условие задачи и решим ее.| Дано: Р = 100 Вт t = 6 ч * 30 = 180 ч Тариф - 30 k/кВт*ч | Решение: А=Рt А =100 Вт * 180 ч = 18 000 Вт * ч =18 кВт * ч Стоимость = 30 (к/кВт * ч) * 18 (кВт * ч) = 5 р 40 коп |
| А—? Стоимость — ? | |
Ответ: А = 18 кВт • ч, стоимость = 5 р. 40 к.
Назад | Далее |